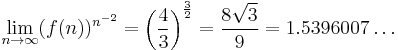Lieb's square ice constant

Binary	1.10001010001000110100010111001100…
Decimal	1.539600717839002…
Hexadecimal	1.8A2345CC0442…
Continued fraction	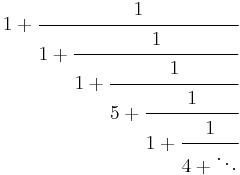$1 %2B \cfrac{1}{1 %2B \cfrac{1}{1 %2B \cfrac{1}{5 %2B \cfrac{1}{1 %2B \cfrac{1}{4 %2B \ddots}}}}}$

Lieb's square ice constant is a mathematical constant used in the field of combinatorics. It was introduced by Elliott H. Lieb in 1967.^[1]

Definition

Let L denote the area of an n × n square lattice, where L = n². Assign a direction to each edge of the lattice. Denote the number of orientations of such that each vertex has two inwardly directed and two outwardly directed edges by f(n).

$\lim_{n \to \infty}(f(n))^{n^{-2}}=\left(\frac{4}{3}\right)^\frac{3}{2}=\frac{8 \sqrt{3}}{9}=1.5396007\dots$

Some historical and physical background can be found in the article Ice-type model.

References

^ Lieb, Elliott (1967). "Residual Entropy of Square Ice". Physical Review 162 (1): 162. doi:10.1103/PhysRev.162.162.